Sorting in Parallel

The problem

The last assignment of my parallel programming class in Spring 2018 involved parallelizing a recursive algorithm. We had no constraints on how we were to parallelize the algorithm other than using C and MPI to do it. Without going into too much detail about the assignment, the main idea of the algorithm was to optmize a cost function based on the datapoint of interested and other “near” points. However, the input data provided was an absolute was compeltely unsorted.

Approach

So, the approach my partner and I wrote had 2 phases:

1. Sort the data in parallel
2. Calculate the cost function, dividing work among the processors

I’m only going into detail on the parallel sorting for a couple of reasons. Sorting in parallel was my major contribution and secondly, I can talk about that aspect without going into any specifics of the assignment since it will likely be used again.

Sorting

Sorting data is a very common topic in Computer Science classes, so I’m not going to spend much time here talking about it, but there are a couple of reasons why I chose to paralelize mergesort.

1. Mergesort lends itself easily to parallelization because it is a divide-and-Conquer algorithm.
2. Our main goal was to show a performance improvement at many different problem sizes, and mergesort’s computational complexity (best, worst, and average) is \(O(n logn)\). In order to achieve this performance profile, mergesort trades off in terms of memory space, but this was not a concern for our application.
3. Mergesort is very easy to visualize, and is pretty simple to write.

Mergesort

Mergesort is typically written as a recursive function which creates a binary tree in the call-stack as shown in the image below from this Techie Delight tutorial on Mergesort.

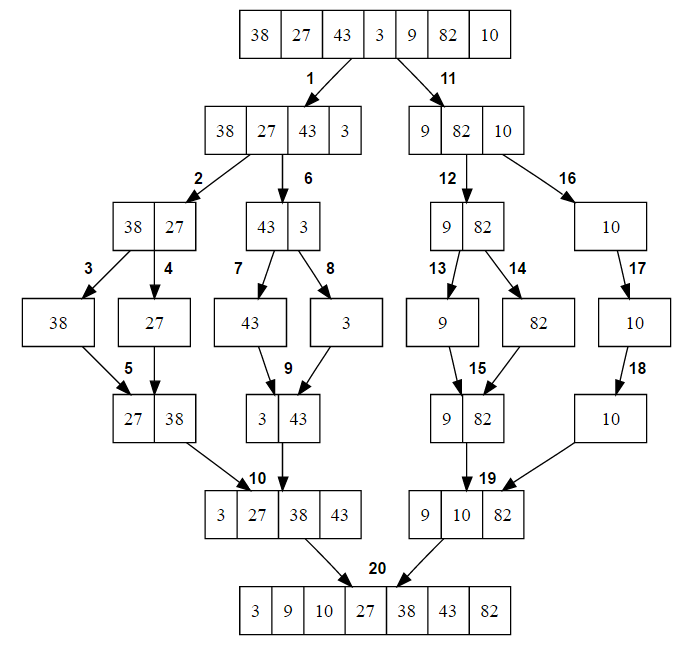
As the algorithm divides up the work, it creates smaller and smaller instances of the exact same problem to solve. That’s why mergesort is so easy to describe recursively. Once it reaches a “base case” (e.g. an array of a single element) that is “trivially” sorted, the process of merging elements back together can begin.

In terms of parallelization, each level of the tree in the image above describes a different number of processors that can be used to sort. As the algorithm breaks in problem down toward the base case, more and more processors can be used. As it builds the sorted array back up, the sections that can be executed in parallel decrease by a factor of 2 each time.

The following function defines the number of procesors, assigns them IDs, and determines at the how much work should be assigned to each processor. For our use-case, each processor was assigned a subset of the total array based on its processor ID. This is called a static block scheduling.

Each processor performs a merge sort on its assigned section of the array, then the sorted segments are sent to another processor to build a larger sorted array. This approach to work distribution was chosen because the smallest input was guaranteed to be more elements than our maximum number of processors. Thus, each processor must be responsible for at least several elements and the dataflow we adopt is that each processor gets a unique slice of the input and performs as shown in Figure 1. Then, all of these segments are merged together efficiently in a tree structure as in the bottom half of Figure 1.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
void Mergesort(unsigned int* arr, unsigned int* arr_out)
{
    int numprocs, myid, elements_per_proc;
    int start, end, i;

    MPI_Comm_size(MPI_COMM_WORLD,&numprocs);
    MPI_Comm_rank(MPI_COMM_WORLD,&myid);

    elements_per_proc = NUM_ELEMENTS / numprocs;

    start = myid * elements_per_proc;
    end = (myid+1) * elements_per_proc;

    //mergesort_helper handles the divide portion in parallel
    mergesort_helper(start, end, arr);
    move_data(arr, arr_out);

    i = 0;
    MPI_Status recv_status;
    int index_change = elements_per_proc;

    //Merge them back together in log2 steps
    while(i < (unsigned int)log2(numprocs)) //merge among all processors
    {
        //destination of where to send is 2^i, where i is the number of iterations
        if (myid % (unsigned int)pow(2,i+1) == 0)
        {
            unsigned int sender = myid + pow(2,i);
            MPI_Recv((void*)&(arr_out[end]), elements_per_proc*(int)pow(2, i), MPI_INT, sender, 0, MPI_COMM_WORLD, &recv_status);

            end += index_change;
            index_change <<= 1;
            merge(arr_out, start, end, ((start+end)/2));
        }
        else //the processor is a sender
        {
            unsigned int receiver = myid - pow(2,i);
            MPI_Send((void*)&(arr_out[start]), elements_per_proc*(int)pow(2, i), MPI_INT, receiver, 0, MPI_COMM_WORLD);

            i = (unsigned int)log2(numprocs);
        }

        i++;
    }
}

This functions manages the single threaded Mergesort. If a processor is assigned more than 2 elements, it will recursively divide and merge the input array until the processor has sorted its work allocation.

1
2
3
4
5
6
7
8
9
10
11
12
13
void mergesort_helper(int start, int end, unsigned int* arr)
{
    unsigned int middle = (start + end) >> 1;

    if(start < middle)
    {
        mergesort_helper(start, middle, arr);

        mergesort_helper(middle, end, arr);

        merge(arr, start, end, middle);
    }
}

The merge function is the sorting actually happens, and unchanged from a typical single-threaded implementation. An array of two sorted halfs are given as input and the halves are copied into temporary arrays so as to not overwrite the values. As long as there are items in both halves, the two top items are compared. The first item is taken and placed into the sorted array.

If one of the halves becomes empty, the remaining half is appended to the sorted array. Now twice the number of items are sorted.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
void merge(unsigned int* arr, unsigned int start, unsigned int end, unsigned int middle)
{
    //find the size of the left subarray and right subarray
    unsigned int left_array_size = middle - start;
    unsigned int right_array_size = end-middle;

    //declare temporary arrays for the sub-arrays
    unsigned int arr_left[left_array_size];
    unsigned int arr_right[right_array_size];

    int i,j;
    //load values into temporary arrays
    for(i=0; i < left_array_size; i++)
    {
        arr_left[i] = arr[i + start];
    }

    for(j=0; j < right_array_size; j++)
    {
        arr_right[j] = arr[middle + j];
    }

    unsigned int sorted_posn = start;
    unsigned int left = 0;
    unsigned int mid = 0 ;
    //look at the head of both piles, take the element that should come first and place in the output array. Increment the index in the pile that was taken.
    while(left < left_array_size && mid < right_array_size)
    {
        //take next from the left pile
        if (arr_left[left] <= arr_right[mid])
        {
            arr[sorted_posn] = arr_left[left];
            left++;
            sorted_posn++;
        }
        else //take next from the right pile
        {
            arr[sorted_posn] = arr_right[mid];
            mid++;
            sorted_posn++;
        }
    }

    //if the right pile is now empty, drain the left pile
    while(left < left_array_size)
    {
        arr[sorted_posn] = arr_left[left];
        left++;
        sorted_posn++;
    }
    //if the left pile is now empty, drain the right pile
    while(mid < right_array_size)
    {
        arr[sorted_posn] = arr_right[mid];
        mid++;
        sorted_posn++;
    }
}

As the merging continues in parallel at each level across processors, the number of sorted elements doubles until finally there is a single sorted array.