Sudoku, Covering Problems, and Logic Design

|

Since starting college, I’ve been flying more regularly between home and school. To pass some of that time, I started doing Sudoku puzzles, but I rather quickly moved from being interested in solving the puzzles themselves to being interesting in algorithms to generate and solve them.

Constraints

  • Start from an empty board when generating a puzzle.
    • While there are numerous transformations that can be applied to a single solved puzzle to generate many “new” ones, doing so seems to defeat the idea of building a program that could generate a Sudoku puzzle as it requires that you already have one.
  • Treat solving a puzzle the exact same as generating a new one.
    • Consider generation of a Sudoku puzzle to be the generalization of solving one.
  • An algorithm that is functional and easily understandable.
    • Efficiency often comes at the price of readability, so for now readability is the priority. In the future, I may revisit this with a more sophisticated algorithm.

Approach

There are many different algorithmic and mathematical approaches to Sudoku, but the depth-first backtracking algorithm seems to best fit the constraints. However, if there is one thing worth noting it is that Sudoku is NP-Complete and as such, depth-first search will have an extremely large solution space to search.

  1. Zero will represent an unassigned cell.
  2. If the grid contains all zeros, a new Sudoku puzzle will be generated.
    1. Numbers 1-9 will be placed randomly in the first row.
  3. If there is an existing puzzle, search for its solution.

The Depth-First Backtracking Algorithm

  1. Advancing row-wise from the top-left, place the lowest valid number into the cell.
  2. Go to the next open cell.
  3. If there are no valid numbers, go back to the previous cell and place the next smallest valid number.
  4. If there is no valid number at this cell, delete its value and go back to the previous cell.
Figure 1: Generating a Sudoku puzzle using depth-first backtracking.

The algorithm generates a solution from scratch in an acceptable time-frame. In this case, the algorithm finishes when it reaches a leaf at the bottom level of the tree (where all 81 numbers are placed.) However, when solving a given Sudoku puzzle, there (usually) just a single leaf that must be found. Furthermore, in this scenario there are certain nodes (valued cells) that must be part of the solution.

**INFO:** There is still a bug on the site which only permits a single p5.js canvas to exist on a given page. The rest of the visuals here are .gif screen recordings of the relevant script.
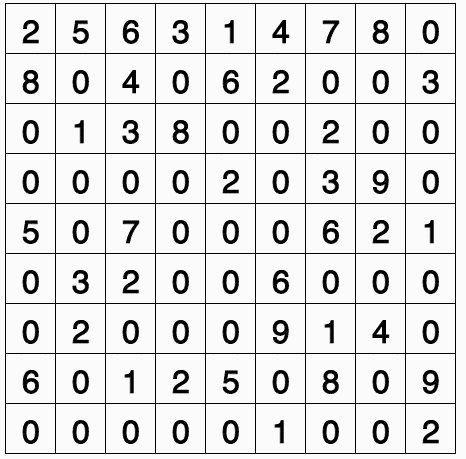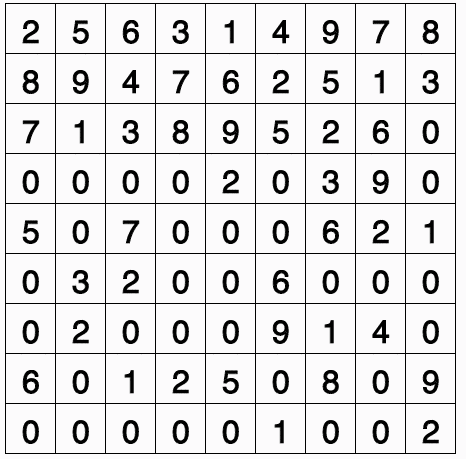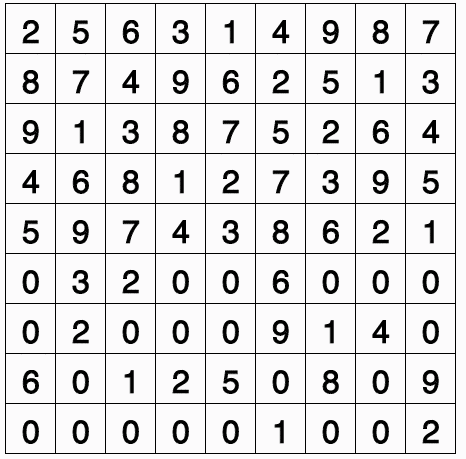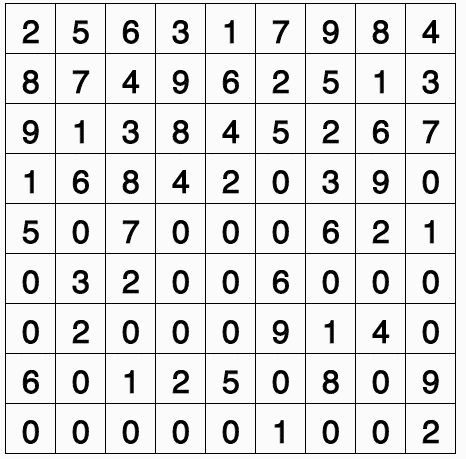
sudoku9_solve
Figure 2: Solving an existing Sudoku puzzle.

To further illustrate the limitations of the depth-first solution, I extended the code to allow for a 16x16 game of Sudoku (using hexadecimal for a bit of extra fun.) The extension from 9x9 to 16x16 expands the grid from 81 numbers to 256 numbers. This dramatically increases the size of the search tree and prevents the depth-first backtracking algorithm from generating a solution in any reasonable time-frame.

sudoku16
Figure 3: Generating a 16x16 Sudoku Puzzle using depth-first backtracking.

Although “Hexadecimal” Sudoku may be rather useless, there are many engineering tasks that require solutions to large NP-Complete problems.

Digital Logic Design

Sudoku is an example of an exact covering problem, but in terms of Digital Logic Design, solutions for unate (for logic minimization) and binate (for technology mapping) are extremely important steps in logic synthesis.